24. 树形与扁平数据结构转换

经典的面试题，首先来分析分析啥是树形和扁平数据结构。

1. 何为树形和扁平数据结构

1.1 扁平化数据结构

扁平化结构的数据如下所示：

let array = [
  { id: 1, name: '1', pid: 0 },
  { id: 2, name: '2', pid: 1 },
  { id: 3, name: '3', pid: 1 },
  { id: 4, name: '4', pid: 3 },
  { id: 5, name: '5', pid: 3 }
]

1
2
3
4
5
6
7

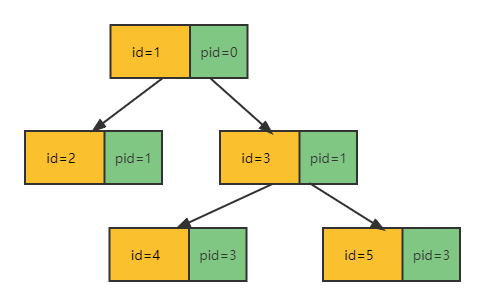
id 标识当前节点
pid 是当前节点的父节点的 id

例如节点 { id: 2, name: '2', pid: 1 }，它的唯一标识 id 是 2，它的 pid 为 1，意味着它的父节点是 id=1 的节点，也就是第一个节点。

1.2 树形数据结构

分析了以上节点属性与节点关系之后，我们能很快理解下面这个由此转换而来的树形结构 tree：children 里面的就是当前节点的子节点，若无子节点，则为空数组。

const tree = [
  {
    id: 1,
    name: '1',
    pid: 0,
    children: [
      {
        id: 2,
        name: '2',
        pid: 1,
        children: []
      },
      {
        id: 3,
        name: '3',
        pid: 1,
        // 省略一些属性
        children: [{ id: 4, ..., pid: 3 }, {id: 5, ..., pid: 3 } ]
      }
    ]
  }
]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

图示如下：

2. 树形结构 => 扁平结构

树形结构数据转扁平结构，思路和多维数组扁平化类似。

从根节点开始，遍历当前节点，把 id、name、pid 属性取出，组成新节点 newNode 加入结果集中；
然后继续递归查找当前节点取出的 children
由于使用了尾递归方法，因此继续传入 array

const treeToArray = (tree, array = []) => {
  for (let node of tree) {
    const { children, ...newNode } = node
    array.push(newNode)
    treeToArray(children, array)
  }
  return array
}

1
2
3
4
5
6
7
8

调用方式：

treeToArray(tree)

3. 扁平结构 => 树形结构

思路：遍历 array，寻找父节点的所有子节点（根据 node.pid === id 判断，node 是被寻找的子节点），每找到一个就加入到当前父节点中，然后给这个父节点创建新属性 children=[]，继续递归查找找每个被加入的新节点 newNode 的子节点。

arrayToTree(array, id, tree) 表示从原来的扁平结构数据中查找 id 节点的所有子节点，并将结果加入到 tree 中。

const arrayToTree = (array, id, tree) => {
  array.forEach(node => {
    if (node.pid === id) {
      const newNode = { ...node, children: [] }
      tree.push(newNode)
      arrayToTree(array, newNode.id, newNode.children)
    }
  })
  return tree
}

1
2
3
4
5
6
7
8
9
10

调用方式：

// 原始数据
// id 标识当前节点，pid 是当前节点的父节点
let array = [
  { id: 1, name: '1', pid: 0 },
  { id: 2, name: '2', pid: 1 },
  { id: 3, name: '3', pid: 1 },
  { id: 4, name: '4', pid: 3 },
  { id: 5, name: '5', pid: 3 }
]

// 初次传入 0，表示从树的根部节点开始生成树结构
arrayToTree(array, 0, [])

1
2
3
4
5
6
7
8
9
10
11
12

24. 树形与扁平数据结构转换 #

1. 何为树形和扁平数据结构 #

1.1 扁平化数据结构 #

1.2 树形数据结构 #

2. 树形结构 => 扁平结构 #

3. 扁平结构 => 树形结构 #