I Don't Know JS

Appearance

Return to top
On this page

03. 二叉树遍历模板

以下代码基于此二叉树节点数据结构：

js
function TreeNode(val, left, right) {
  this.val = (val === undefined ? 0 : val)
  this.left = (left === undefined ? null : left)
  this.right = (right === undefined ? null : right)
}
1
2
3
4
5

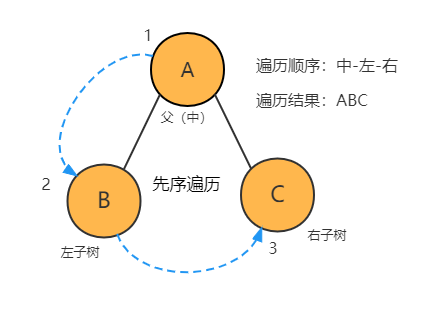
1. 先序遍历

1.1 先序遍历（递归）

先序遍历顺序按照 中(父)-左子树-右子树 的顺序遍历节点。

j9N0C8.png

js
const preOrder = (node, res = []) => {
  if (node) {
    res.push(node.val)        // 中（父节点）
    preOrder(node.left, res)  // 左子树
    preOrder(node.right, res) // 右子树
  }
  return res
}
1
2
3
4
5
6
7
8

1.2 先序遍历（迭代）

js
const preOrder = (node) => {
  if (!node) return []
  const res = []
  const stack = [node]
  while (stack.length) {
    const n = stack.pop()
    res.push(n.val)
    n.right && stack.push(n.right) // 右先进，先入后出
    n.left && stack.push(n.left) // 左后进，后进先出
  }
  return res
}
1
2
3
4
5
6
7
8
9
10
11
12

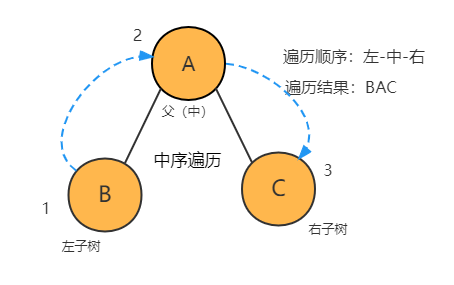
2. 中序遍历

2.1 中序遍历（递归）

中序遍历顺序按照 左子树-中(父)-右子树 的顺序遍历节点。（前序基础上，修改一下访问节点的顺序即可）

j90w6O.png

js
const inOrder = (node, res = []) => {
  if (node) {
    inOrder(node.left, res)  // 左子树
    res.push(node.val)        // 中（父节点）
    inOrder(node.right, res) // 右子树
  }
  return res
}
1
2
3
4
5
6
7
8

2.2 中序遍历（迭代式）

js
function inorderTraversal( root ) {
   if (!root) return []
   let res = []
   let stack = []
   let cur = root
   while(cur || stack.length) {
       while(cur) {
           stack.push(cur)
           cur = cur.left
       }
       let node = stack.pop()
       res.push(node.val)
       cur = node.right
   }
   return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

3. 后序遍历

3.1 后序遍历（递归）

后序遍历顺序按照 左子树-右子树-中(父) 的顺序遍历节点。

js
const inOrder = (node, res = []) => {
  if (node) {
    inOrder(node.left, res)  // 左子树
    inOrder(node.right, res) // 右子树
    res.push(node.val)        // 中（父节点）
  }
  return res
}
1
2
3
4
5
6
7
8

3.2 后序遍历（迭代）

仿照先序遍历，修改为 根右左，因为后序遍历是 左右中，所以反转数组即可。

js
const preOrder = (node) => {
  if (!node) return []
  const res = []
  const stack = [node]
  while (stack.length) {
    const n = stack.pop()
    res.push(n.val)
    n.left && stack.push(n.left) // 左后进，后进先出
    n.right && stack.push(n.right) // 右先进，先入后出
  }
  return res.reverse()
}
1
2
3
4
5
6
7
8
9
10
11
12

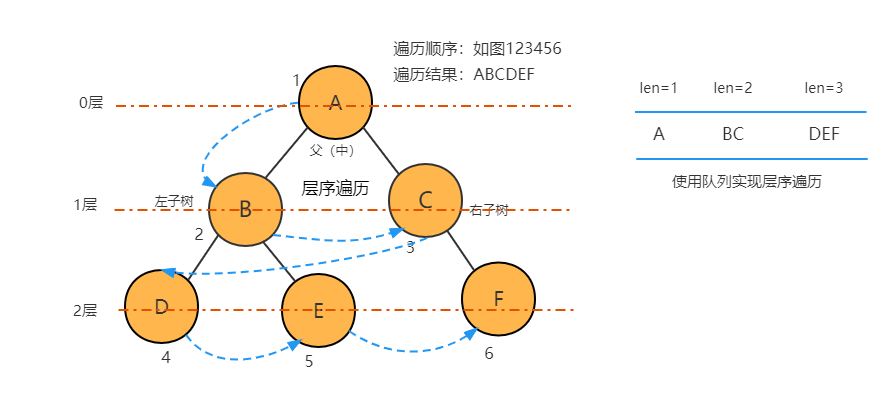
4. 层序遍历

使用队列实现二叉树的层序遍历，外层 q.length 循环，使用 len 记录外层循环开始时队列 q 中的节点数量，内层循环 len 次，将同层级的节点值保存到同一数组中，同时将下一层的左右子树入队列 q。结合图示阅读代码更好理解。

层序遍历.png

js
const levelOrder = function (root) {
  if (!root) return []
  let q = [root], ans = []
  while (q.length) {
    let len = q.length
    let temp = []
    while (len--) {
      let node = q.shift()
      temp.push(node.val) // 每层节点值存入同一个数组
      node.left && q.push(node.left)
      node.right && q.push(node.right)
    }
    ans.push(temp) // 同层节点形成的数组存入新数组，形成二维数组
  }
  return ans
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

层序遍历求树最大深度

层序遍历可以求每一层的节点，也就意味着可以求二叉树的最大深度。

js
function maxDepth( root ) {
  if (!root) return 0
  let res = 0, queue = [root]
  while(queue.length) {
    let len = queue.length
    while(len--) {
      let node = queue.shift()
      node.left && queue.push(node.left)
      node.right && queue.push(node.right)
    }
    res++
  }
  return res
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14

也可以使用递归解决：

js
function maxDepth( root ) {
  if (!root) return 0
  return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1
}
1
2
3
4